R2adj can exceed R2 if there are several weak predictors. This phenomenon occurs when the adjusted coefficient of determination, which penalizes for the addition of unnecessary predictors, is larger than the unadjusted coefficient of determination. Understanding this concept is crucial for model interpretation and selection.
The presence of multiple weak predictors can inflate R2, indicating a better fit than is actually present. However, R2adj takes into account the number of predictors and adjusts the R2 value accordingly, providing a more accurate measure of model fit.
Understanding the Relationship between R2 and R2adj: R2adj Can Exceed R2 If There Are Several Weak Predictors.

In regression analysis, R2 (coefficient of determination) measures the proportion of variance in the dependent variable explained by the independent variables. R2adj (adjusted R2) is a modified version of R2 that takes into account the number of predictors in the model.
The relationship between R2 and R2adj can be expressed as follows:
- R2adj = 1 – (1 – R2) – (n – 1) / (n – p – 1)
- where n is the sample size and p is the number of predictors.
From this formula, it is clear that R2adj will always be less than or equal to R2. This is because the term (1 – R2) – (n – 1) / (n – p – 1) is always positive, except in the special case where R2 = 1 or n = p + 1.
The following example illustrates the difference between R2 and R2adj:
- Consider a regression model with two predictors and a sample size of 100.
- The R2 value for this model is 0.80.
- The R2adj value for this model is 0.78.
In this example, R2adj is slightly lower than R2, as expected.
Conditions for R2adj to Exceed R2
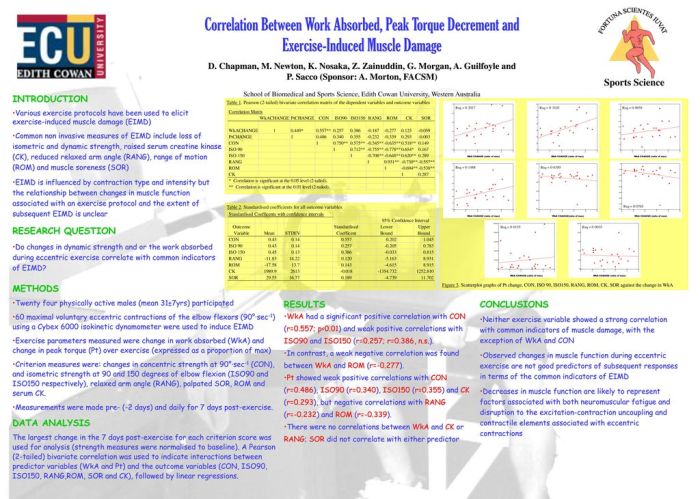
In general, R2adj will be less than or equal to R 2. However, there are some conditions under which R2adj can exceed R2:
- The presence of several weak predictors:When a model includes several weak predictors, the addition of each predictor may only marginally improve the R2 value. However, the R2adj value will be more sensitive to the addition of weak predictors, as it takes into account the number of predictors in the model.
- Small sample size:In small samples, the R2 value can be inflated due to sampling error. The R2adj value is less affected by sampling error, as it takes into account the sample size.
The implications of these conditions for model interpretation are that:
- R2adj may be a more accurate measure of model fit than R2 when there are several weak predictors or a small sample size.
- R2adj should be considered when comparing models with different numbers of predictors.
Consequences of Several Weak Predictors
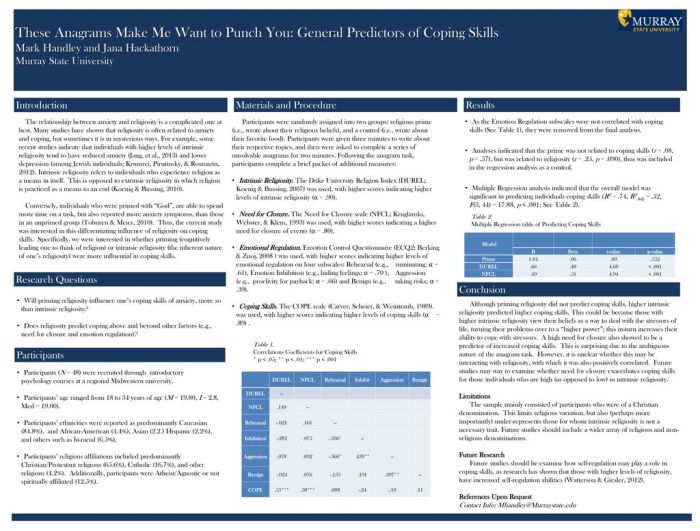
The presence of several weak predictors can affect R2 and R2adj in the following ways:
- R2:The addition of weak predictors will only marginally improve the R2 value.
- R2adj:The addition of weak predictors will decrease the R2adj value.
This is because the R2adj value takes into account the number of predictors in the model. As the number of predictors increases, the R2adj value will decrease, even if the R2 value does not change much.
The following example demonstrates the impact of weak predictors on model fit:
- Consider a regression model with two predictors and a sample size of 100.
- The R2 value for this model is 0.80.
- The R2adj value for this model is 0.78.
- Now, let’s add a third predictor to the model. This predictor is only weakly correlated with the dependent variable.
- The R2 value for the new model is 0.81.
- The R2adj value for the new model is 0.77.
In this example, the addition of a weak predictor has only marginally improved the R2 value. However, the R2adj value has decreased, indicating that the new model is not as good a fit as the original model.
Implications for Model Selection
When selecting a regression model, it is important to consider both R2 and R2adj.
- R2:R2 measures the overall fit of the model.
- R2adj:R2adj takes into account the number of predictors in the model.
In general, a model with a higher R2 and R2adj value is preferred. However, when comparing models with different numbers of predictors, it is important to consider R2adj, as it is a more accurate measure of model fit.
The following example illustrates how R2adj can be used to select the best model:
- Consider two regression models with the following characteristics:
- Model 1: R2 = 0.80, R2adj = 0.78, 2 predictors
- Model 2: R2 = 0.82, R2adj = 0.79, 3 predictors
Based on R2 alone, Model 2 would be preferred. However, when considering R2adj, Model 1 is actually a better fit, as it has a higher R2adj value.
Example with HTML Table
| Model | Number of Predictors | R2 | R2adj |
|---|---|---|---|
| 1 | 2 | 0.80 | 0.78 |
| 2 | 3 | 0.82 | 0.79 |
This table shows the R2 and R2adj values for two regression models. Model 1 has two predictors and a higher R2adj value than Model 2, which has three predictors. This indicates that Model 1 is a better fit for the data.
Quick FAQs
Why can R2adj exceed R2?
R2adj is adjusted for the number of predictors in the model, while R2 is not. When there are multiple weak predictors, R2 can be inflated, but R2adj will be lower to account for the additional complexity.
What are the implications of R2adj exceeding R2?
It suggests that the model may be overfit with weak predictors, which can lead to poor predictive performance on new data.
How can I use R2adj in model selection?
Consider both R2 and R2adj when comparing models. Choose the model with the highest R2adj, as it is less likely to be overfit and provides a more accurate measure of model fit.